时间:2023-11-28 11:35
人气:
作者:admin
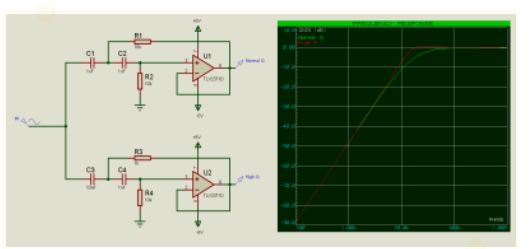
有源滤波器将有源元件引入滤波电路;有源元件是由外部电源而不是信号本身单独供电的元件。通过在滤波器后增加一个缓冲运算放大器,我们可以用无衰减的信号驱动更高的负载;例如下面的高通滤波器示例:
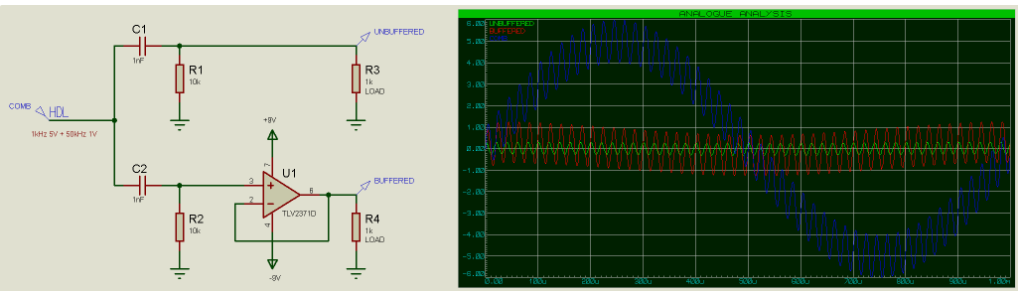
请注意,与缓冲输出(红色走线)相比,无缓冲输出(绿色走线)如何显著衰减。
为什么要使用有源元件?
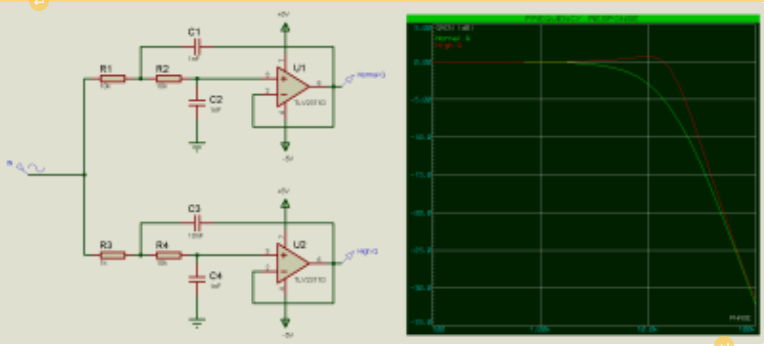
在高阶滤波器链中添加缓冲器还会降低该链中每个链路之间的衰减,并防止该链中的滤波器元件扭曲该链中其他滤波器元件的滤波器特性。以下面的二阶低通滤波器为例,我们可以看到,第二个滤波器看到的阻性元件不仅仅是R2=10k,而是R1 + R2 = 20k,第一个滤波器看到的电容不仅仅是C1的电容,还需要考虑C2的电容。
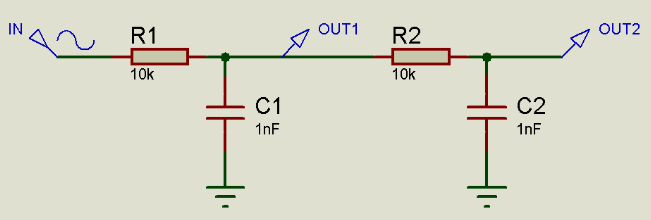
鉴于
Cutoff Frequency = 1/2πRC这具有降低滤波器截止频率的效果。
这具有降低滤波器截止频率的效果。
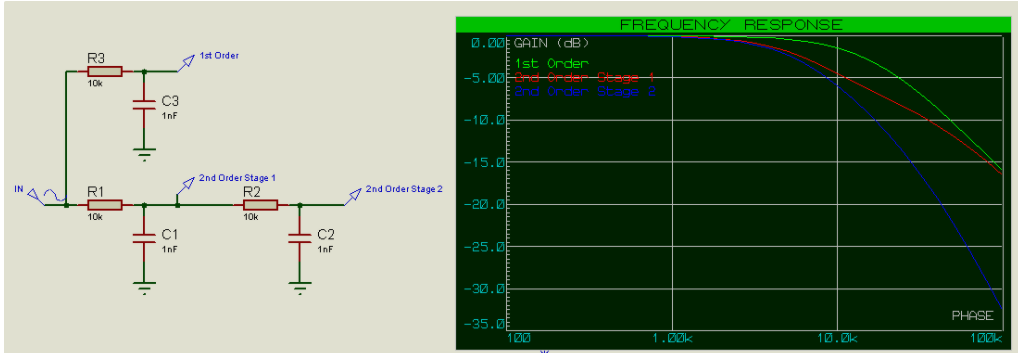
对于10k和1nF的R和C值,我们预计截止频率为15.9kHz(第一滤波器级为-3dB,第二滤波器级为-6dB),但我们发现它比这个数字要低一些。请注意,二阶1级的频率响应最初如何跟随二阶2级的频率响应,因为在低频时,电容充当开路(就好像它们不存在一样),然而在较高频率时,二阶1级的频率响应则跟随一阶滤波器的频率响应,因为C1开始充当与R2相比具有较低电阻的短路。
如果我们在滤波器第二级中降低电阻并增加电容(但保持RC不变),这种情况会更加明显:
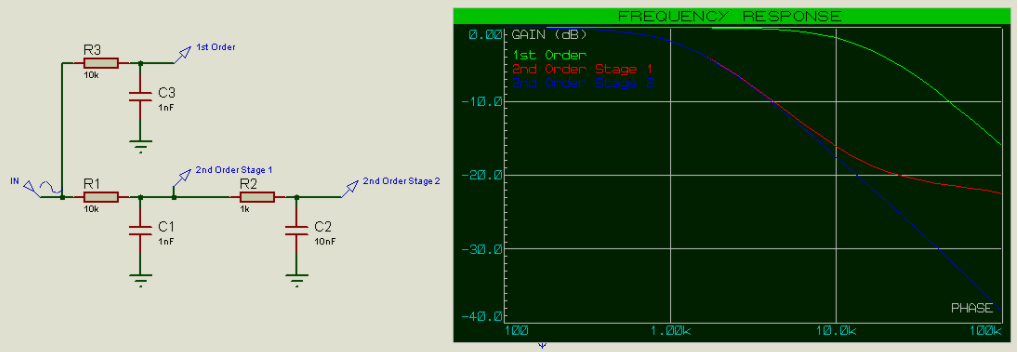
这使得截止频率变得更低。
减轻这一问题的一种方法是使第二级的输入阻抗至少比第一级的输出阻抗大一个数量级(10倍),即使R2比R1大10倍(C2小10倍,从而保持RC不变)。
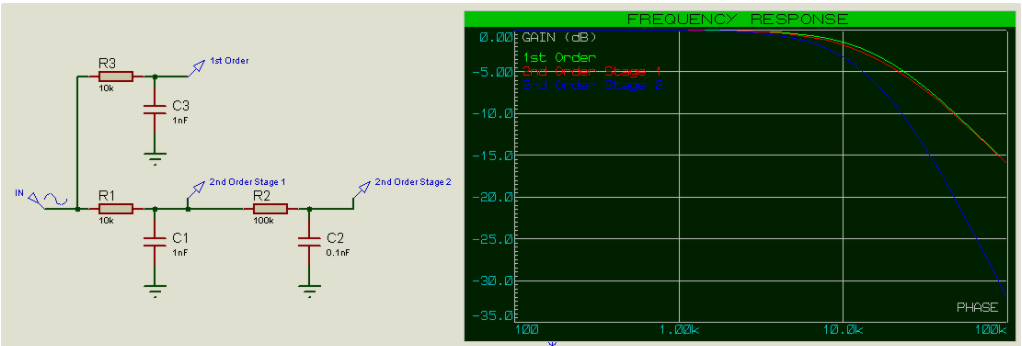
现在我们可以看到,二阶滤波器第1级的频率响应与一阶滤波器的频率响应非常匹配。截止频率也非常接近预期的15.9kHz。
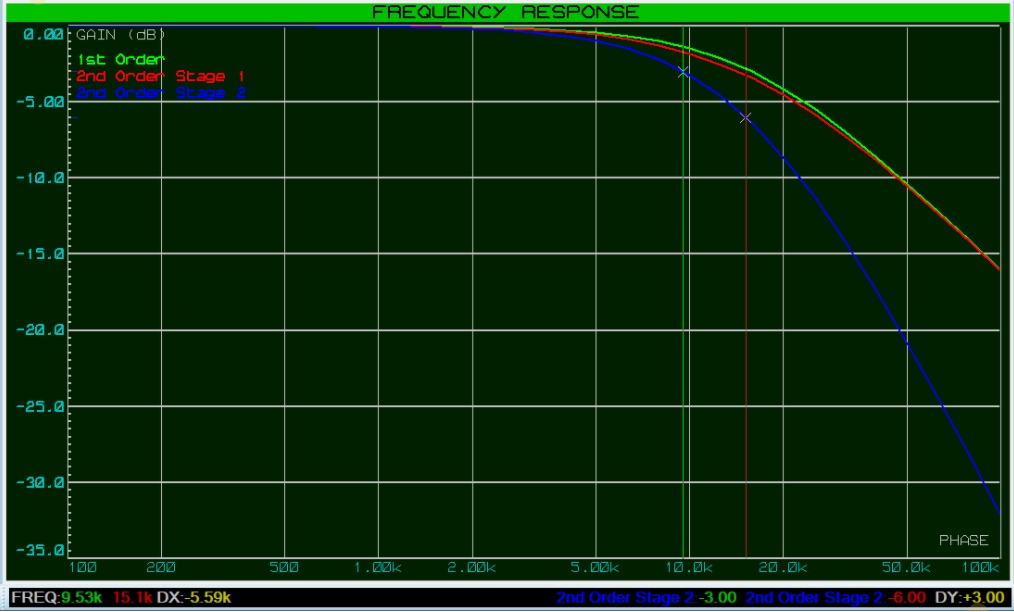
进一步降低第一级的输出阻抗和/或增加第二级的输出阻抗将继续使截止频率更接近预期;然而,它永远不会完全到达那里,并且添加第三(或第四等)滤波器级会使情况进一步复杂化。
而且(终于!)这就是我们引入主动组件的原因。
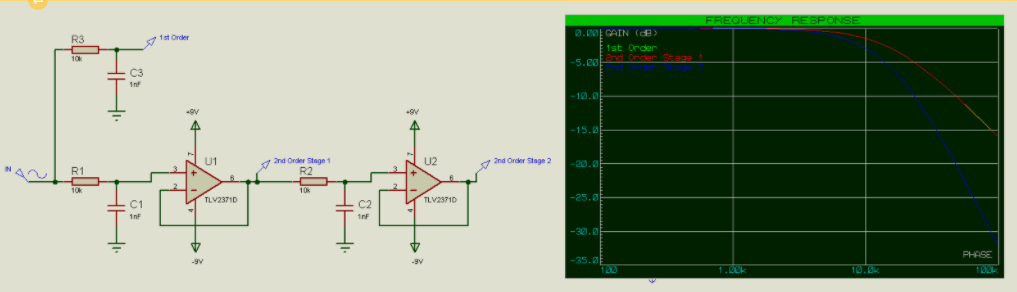
在这种情况下,我们可以看到,二阶滤波器的第1级与一阶滤波器的第1级完全匹配,截止频率为预期的15.9kHz。
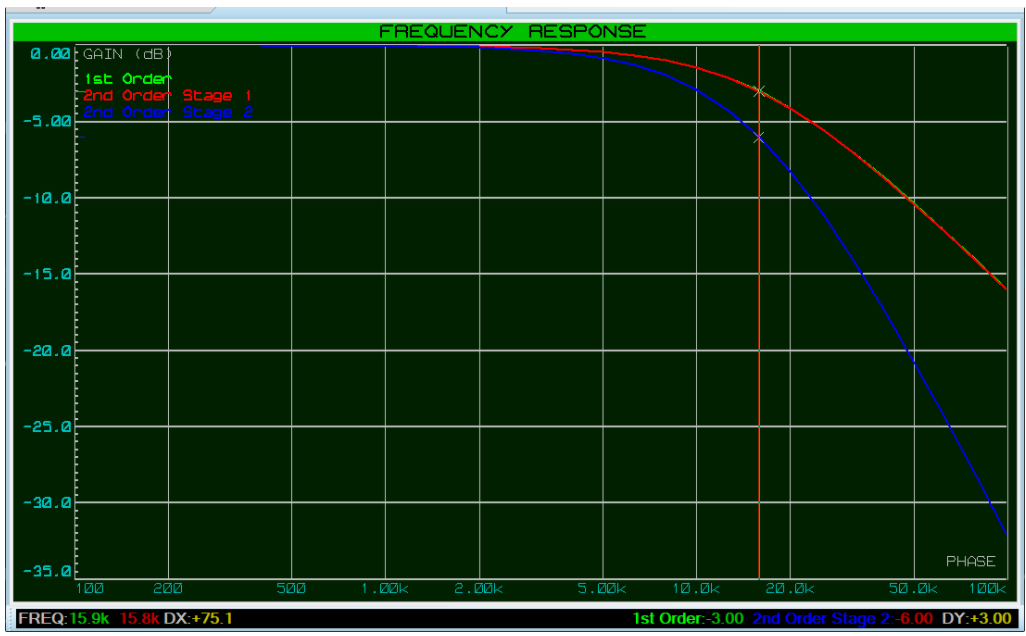
我们可以根据需要轻松添加额外的滤波器级,以获得所需的滚降锐度。
注意,每增加一个滤波器级,截止频率下的衰减以dB为单位增加-3dB。一阶滤波器在截止频率处的衰减为-3dB,二阶滤波器为-6dB,三阶滤波器为-9dB,依此类推。
Sallen-Key拓扑
Sallen-Key拓扑结构是一种流行的二阶滤波器拓扑结构,它使用单个运算放大器(而不是上面提到的两个运算放大器)。
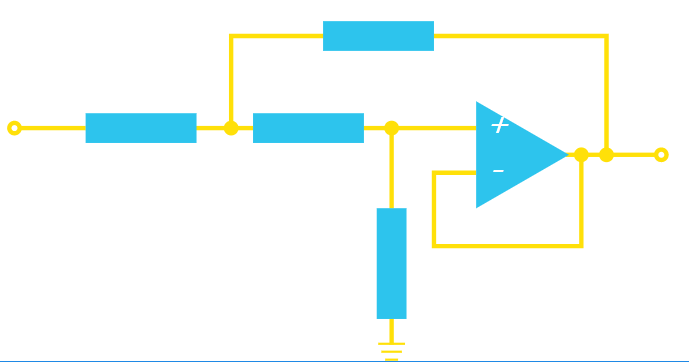
Z元件的选择取决于是否需要低通、高通、带通或带阻滤波器。
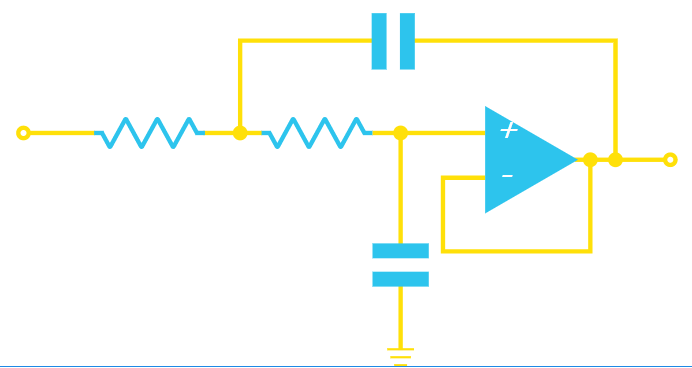
低通Sallen-Key滤波器
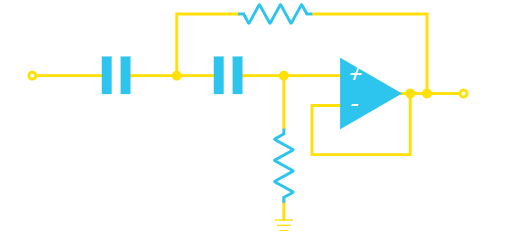
高通Sallen-Key滤波器
也可以选择增加增益(在运算放大器的反相输入端使用分压器):
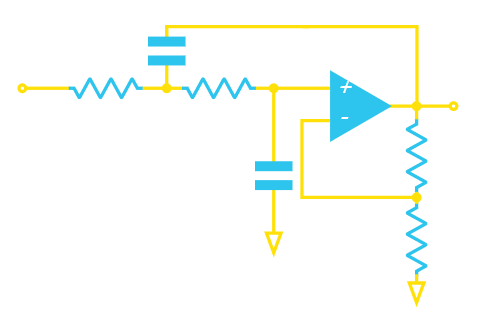
带增益的Sallen-Key滤波器
Sallen-Key滤波器的有趣特性是第一级不接地,而是连接到运算放大器的输出端。这将运算放大器的输出反馈回正输入,可用于提高滤波器的“Q”。
品质因数,Q
在科学上,振荡系统的品质因数或Q描述了它的阻尼程度(或者更确切地说,是指它的欠阻尼程度——与阻尼相反)。在空气中摆动的钟摆比在水中摆动的钟摆具有更高的Q因子;在空中摆动的钟摆在每次摆动时损失的阻力能量较少,因此摆动时间较长。
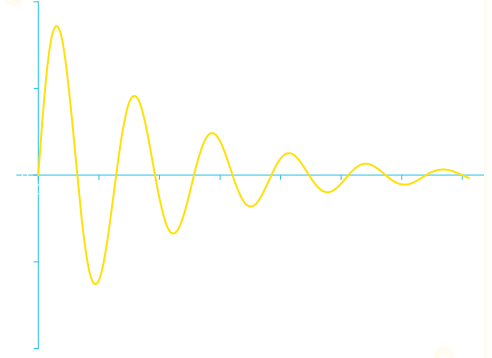
Q = 1表示没有阻尼/欠阻尼,信号幅度保持不变。
Q 》 1意味着信号被放大(增加)。
Q 《 1意味着信号衰减(降低)。
就滤波器响应而言,滤波器的Q描述了它在截止频率(下图中的10kHz)附近的表现:
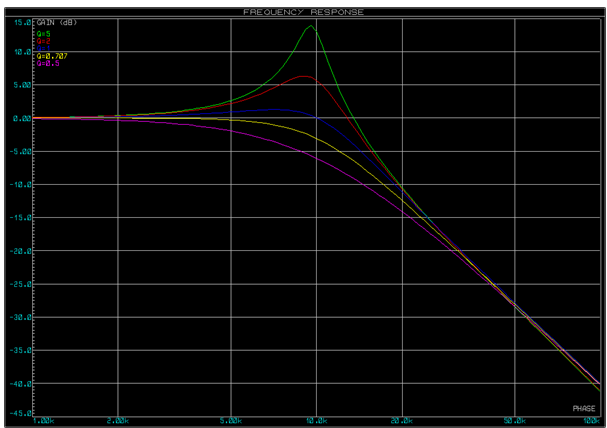
Q 》 1将放大截止频率的信号。
Q = 1将使信号幅度在截止频率保持不变。
Q 《 1将衰减截止频率处的信号。
另请注意,Q值越高,截止频率处的转折越尖锐。无源一阶滤波器的Q值为0.707 (-3dB),无源二阶滤波器的Q值为0.5 (-6dB)。然而,使用Sallen-Key有源滤波器拓扑结构,我们可以为我们的应用选择Q值——例如,我们可能更喜欢Q值为1,这样我们的滤波器可以保持信号在接近截止频率时不衰减,然后在截止频率时具有更急剧的滚降。
其工作原理是,来自输出端的滤波信号反馈到输入信号,在截止频率附近与其谐振,从而提高其幅度(进而提高Q值)。
低通计算
Sallen-Key滤波器背后的数学原理很复杂,深入分析超出了本文的范围。有在线和离线计算器,可以方便地计算给定截止频率、Q和增益的R和C值。不过,我们将简要观察一种简化的情况,其中增益为1(单位),电阻和电容设置为彼此的比值(这与我们迄今为止创建的高阶滤波器类似)。
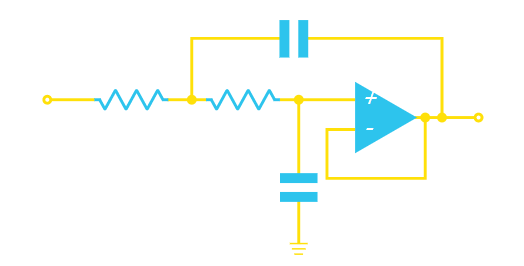
低通Sallen键
Let R2 = xR1, and C2=(1/x)C1.这与我们之前所做的类似(当时我们创建了一个2级无源滤波器来减轻对截止频率的影响),截止频率的公式仍然是1 / 2πRC。
The formula for Q is then x / (x + 1)。由此我们可以看出,如果x=1(两个阶段中的分量值相同),则我们得到1 / (1 + 1) = 1/2 = 0.5的Q;这与我们用普通2级滤波器得到的Q值相同(-6dB)。然而,如果我们将x增加到10,那么我们得到的Q为10/11 = 0.91,这比我们之前得到的要高得多。
高通计算
这里的计算都是一样的,所以还是让R2 = xR1,C2=(1/x)C1。
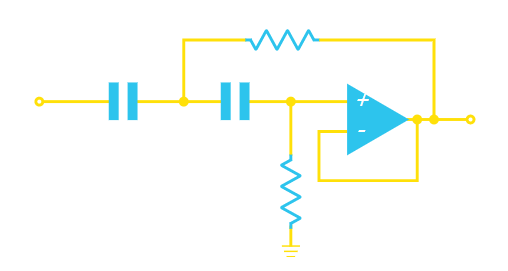
高通Sallen键
对于x = 1,我们再次得到Q = 0.5,对于x = 10,我们再次得到Q = 0.91。
审核编辑:黄飞

https://file1.elecfans.com/web2/M00/A4/CE/wKgZomUMN

https://file.elecfans.com/web1/M00/85/2B/pIYBAFxiNN